|
This approximation is following
the discussion in the book [1].
Let’s consider g(x) is the
distribution of the gain coefficient in the gain element, then the expression
for the amplification of the IR oscillation could be written as
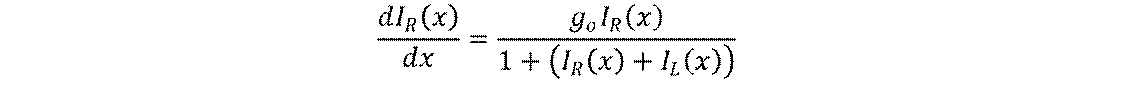
, where g0 is the
gain coefficient for a small signal. An identical equation, but with the sign
reversed and IL(x) replaced by IR(x), is obtained for the wave
traveling in the (−x) direction. By
solving these equations
together, one could obtain that
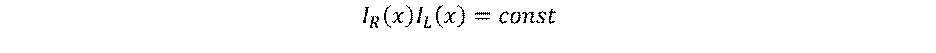
In the case when the
reflectivity of the output mirror is high; in this case variations of IL(x) and
IR(x) as a function of x are
relatively small. If we treat these changes as a perturbation 𝐼𝑅(𝑥) + ∆𝐼
and 𝐼𝐿(𝑥) + ∆𝐼 we obtain, as an
approximation for total intracavity power (𝐼Σ),
𝐼Σ = 𝐼𝑅(𝑥) + 𝐼𝐿(𝑥) ≈ 𝑐onstant
Using this equation at mirror R1 we can get
𝐼Σ = 𝐼𝑅1 + 𝐼𝐿1 = (1 + 𝑅1)𝐼𝑅1
In this case, the circulating
power Icirc is a good approximation equal to the average of the
power densities of the
counterpropagating beams
𝐼circ = (𝐼𝑅 + 𝐼𝐿)⁄2
The above results are basic for
using space-independent rate equations to model laser
characteristics. Using the above
equation for output radiation as
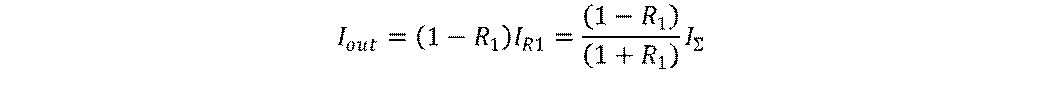
or ratio between 𝐼Σ and 𝐼out will be
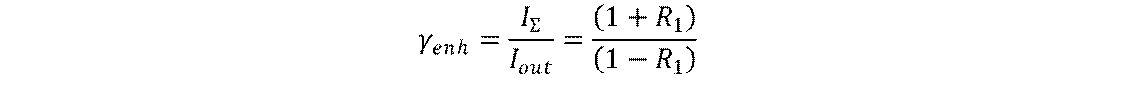
This equation shows how much intracavity power
exceeds output power and as one can see the ratio grows when R1 approaches to
1. The plot of this dependence is shown below
|